Трение от угла

7 февраля 2022. Комментарии .

Классная задача-исследование из динамики:

Кирпич лежит на доске, коэффициент трения о которую равен . Угол наклона доски к горизонту медленно увеличивают. Найти зависимость силы трения, действующей на кирпич, от угла наклона доски.

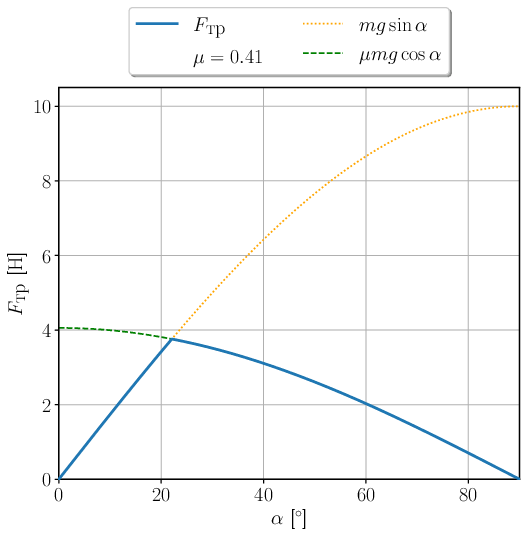
Понятно, что кирпич покоится, когда $т р$ . Когда он начинает скользить, сила трения достигает значения . Смыкаются эти ситуации при (сила трения уже предельна, но кирпич еще не скользит). Все это довольно банальные мысли из динамики, если кому-то хочется рисунков и подробностей — обращайтесь к соответствующей задаче на earthz.ru.

Мне же было любопытно посмотреть, как график выглядит на самом деле. В большинстве идейно правильных решений, имеющихся в интернете в большом количестве, графики нарисованы от руки или только качественно.

Как обычно, я построил график на питоне. И сделал анимацию, показывающую, что меняется в зависимости от коэффициента трения. Довольно много информации зашифровано в этом графике. Например, график позволяет вычислить массу груза. Также хорошо видно, что симметричным график становится при . Так и должно быть, ведь тогда синусоида и косинусоида имеют одинаковую амплитуду и пересекаются на . Излом синей кривой всегда происходит на угле .

Вообще — красиво, что одна кривая скользит по другой и вырезает какую-то ее часть. Щелкните, чтобы запустить анимацию. Сработает с задержкой из-за размера файла.

Можно посмотреть на код графика.

Любопытно, что в большинстве вручную построенных графиков почти всегда преувеличена кривизна синусоиды и косинусоиды. А ведь первый замечательный предел говорит о том, что при малых углах график очень похож на график прямой . Вплоть до 30 градусов визуально синусоида от прямой почти не отличается (если прямую, конечно, не рисовать рядом).