Эллипс против параболы

2 января 2022. Комментарии .

При решении школьных задач по физике очень небольшому проценту учеников удается постоянно держать в голове мысль о том, что мы всегда работаем в рамках некоторой модели, которая дает разумные результаты в ограниченном диапазоне условий.

Оглавление #

Физические модели
Задача

Физические модели #

Вот характерный пример. Вскоре после бесчисленного количества задач на движение брошенного под углом к горизонту тела ученик девятого класса встречается с движением спутника вокруг Земли. И я всегда задаю следующий вопрос — мол, в октябре мы бросали тело под углом к горизонту, и оно двигалось по параболе. Так? Так. А сейчас у нас спутник летит вокруг Земли по окружности (или по эллипсу). Так? Так. А где тот момент, когда камень, брошенный под углом к горизонту, полетит не по параболе, а по эллипсу?

Оказывается, что момента такого нет. В самом деле, движение брошенного под углом к горизонту тела решается в рамках модели бесконечной плоской Земли. У такой Земли, разумеется, и масса бесконечно велика, и ускорение свободного падения мало того что не меняет направления, так еще и не меняет свою величину с высотой. Поэтому в такой модели тело никогда не полетит по эллипсу, а всегда по параболе.

Движение же спутника рассматривается в рамках совершенно другой модели. Тут ускорение меняет и направление, и величину.

У меня возникла идея объединить бросок под углом к горизонту с движением спутников. Получилась весьма необычная по формулировке задача. Но основная ценность задачи оказалась случайным образом в другом — получилась одна из немногих задач на второй закон Кеплера. Я довольно долго занимался олимпиадной астрономией, но сходу ни одной задачи на второй закон не вспомнил. Делитесь в комментариях, если знаете такие задачи.

Задача #

Тело с поверхности однородной планеты радиусом и массой выстреливают под углом к горизонту с первой космической скоростью для данной планеты. Считайте, что планета лишена атмосферы и не вращается. Найдите:

Эксцентриситет орбиты.
Время движения тела.
Максимальное удаление тела от поверхности планеты.

Траектория и положение на ней #

В первую очередь хочется разобраться, как траектория движения тела будет расположена относительно планеты.

Траектория будет иметь форму эллипса, как того требует первый закон Кеплера, а в одном из фокусов эллипса должен располагаться центр тяготения — значит, центр планеты совпадает с фокусом эллипса.

Найдем большую полуось орбиты . В принципе, из ЗСЭ ясно, что круговую скорость (направленную как угодно) тело имеет при удалении на большую полуось от фокуса. Если это не очевидно, можно поступить формально и приравнять круговую скорость к скорости в произвольной точке траектории (в нашем случае эта точка удалена на от фокуса). Занимающимся олимпиадной астрономией эта формула известна как «интеграл энергии»:

откуда . Теперь вспомним, что сумма расстояний от фокусов до произвольной точки эллипса постоянна и равна , поэтому отрезок длиной , проведенный из фокуса , попадает в точку пересечения эллипса с его малой полуосью. Отлично, с траекторией разобрались, можно нарисовать. Эллипс настоящий, график построен на python, можно посмотреть код.

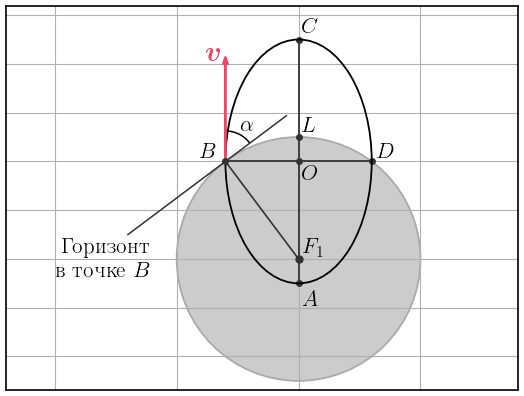
Эксцентриситет #

Эксцентриситет эллипса равен отношению фокусного расстояния к большой полуоси, . Учтем, что скорость направлена по касательной к эллипсу, то есть перпендикулярна , а горизонт направлен по касательной к планете, т.е. перпендикулярен радиусу .

Тогда угол , а , поэтому эксцентриситет . Очень красивый результат.

Время полета #

На помощь приходит второй закон Кеплера: радиус-вектор планеты за равные промежутки времени заметает равные площади. Посмотрим, что он успевает замести (код графика).

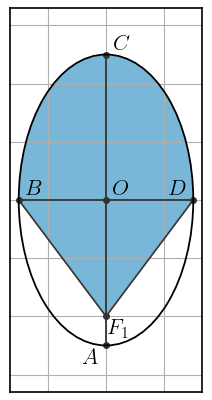
Площадь эллипса , где — малая полуось эллипса. Площадь закрашенного сегмента . Тогда:

Максимальное удаление тела от поверхности планеты #

Любопытно, что максимальная высота подъема равна фокусному расстоянию эллипса.