Геометрическая оптика на карантине
27 апреля 2020. Комментарии .Из-за перехода на онлайн-обучение стал готовить презентации к урокам. Довольно удобно — нажимаешь кнопочку, появляется очередная формула. Делаю презентации в латехе. Если незнакомы с этой системой подготовки документов — очень советую попробовать. Порог вхождения умеренно высок, но результаты замечательные, время тоже с какого-то момента экономится. Слайды сопровождаю графиками, построенными на python.
Для геометрической оптики, которую сейчас изучаем с 8 классом, жанр презентаций оказался, на мой взгляд, подходящим. Посмотрите, например, на вывод формулы тонкой линзы для трёх случаев (надо нажать на картинку, чтобы пошла анимация):
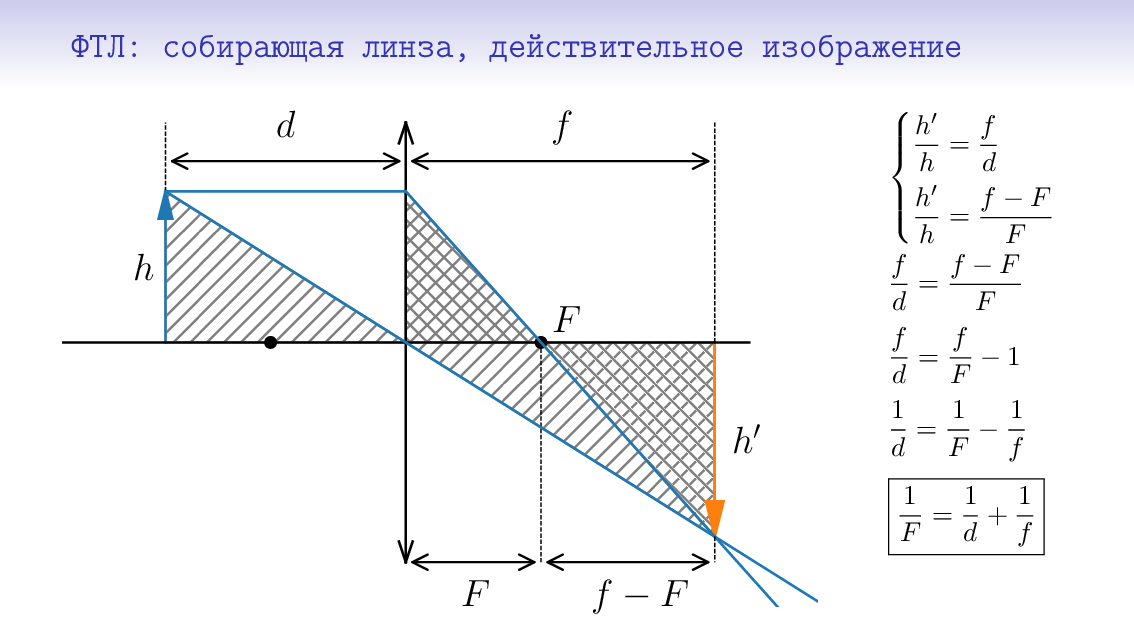
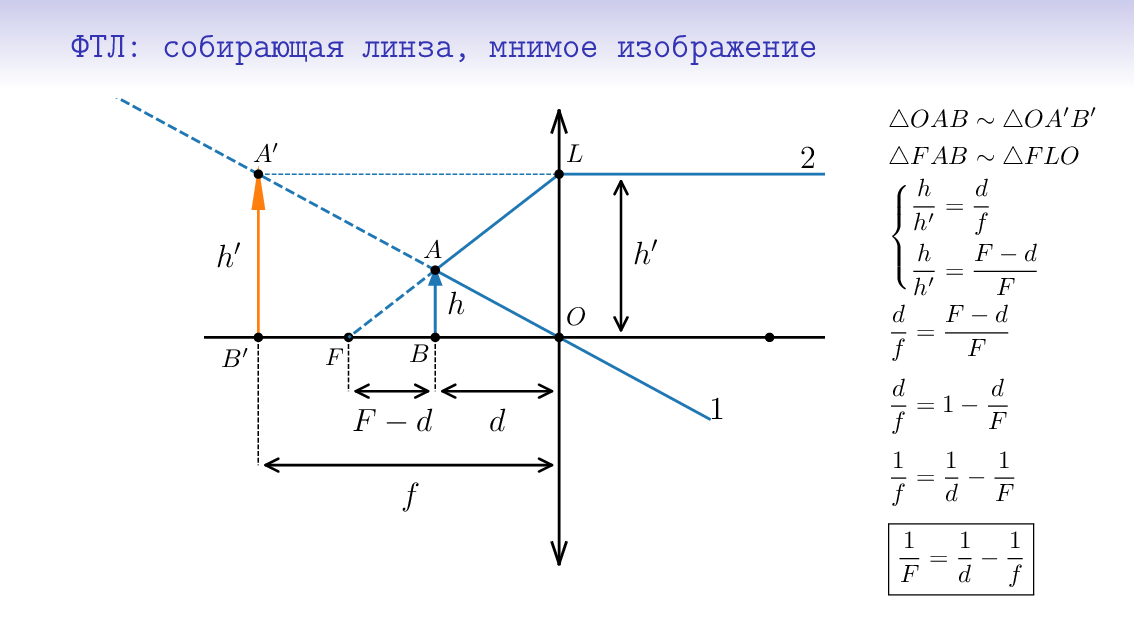
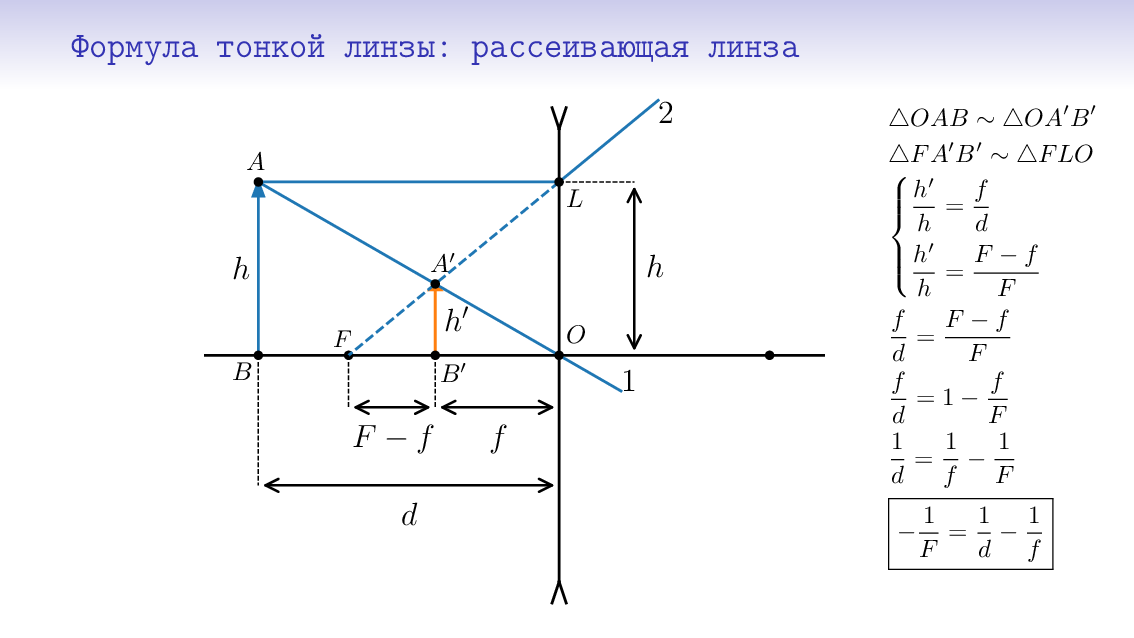
Построены картинки на python. В разумных пределах можно поменять, например, фокусное расстояние, и получится другая картинка, причём все лучи всё ещё будут идти как положено (благо со сферической аберрацией они не знакомы).
Вот скрипты, которые строят показанные картинки, т.е. вывод формулы тонкой линзы для действительного, мнимого увеличенного и мнимого уменьшенного изображений: ftl_sd.py, ftl_sm.py, ftl_r.py.
Однако времени писать полноценную рабочую библиотеку перед уроками, как правило, нет, поэтому написано всё на скорую руку, неоптимально и неудобно. Отличная задача для проекта, посильная для знакомых с ООП школьников — написать библиотеку для построения подобных графиков, чтобы эти же картинки можно было получить за 20, а не за 200 строк. Сейчас аналогичную задачу для построения термодинамических циклов выполняет в рамках школьного проекта один ученик, получается довольно хорошо. Когда будет доведено до ума, буду пользоваться, а пока с интересом слежу за прогрессом проекта.
Кстати, для построения электрических схем на python я пользуюсь замечательной библиотекой SchemDraw.
Напоследок покажу, как выглядят в анимации любопытные задачки на нахождение положения линзы и фокусов по источнику, изображению и оптической оси. В вашем распоряжении линейка без делений и возможность строить прямые, параллельные данной.

